multi-cor (sa-axis)#

../../../_images/saaxis.png

Behavior#

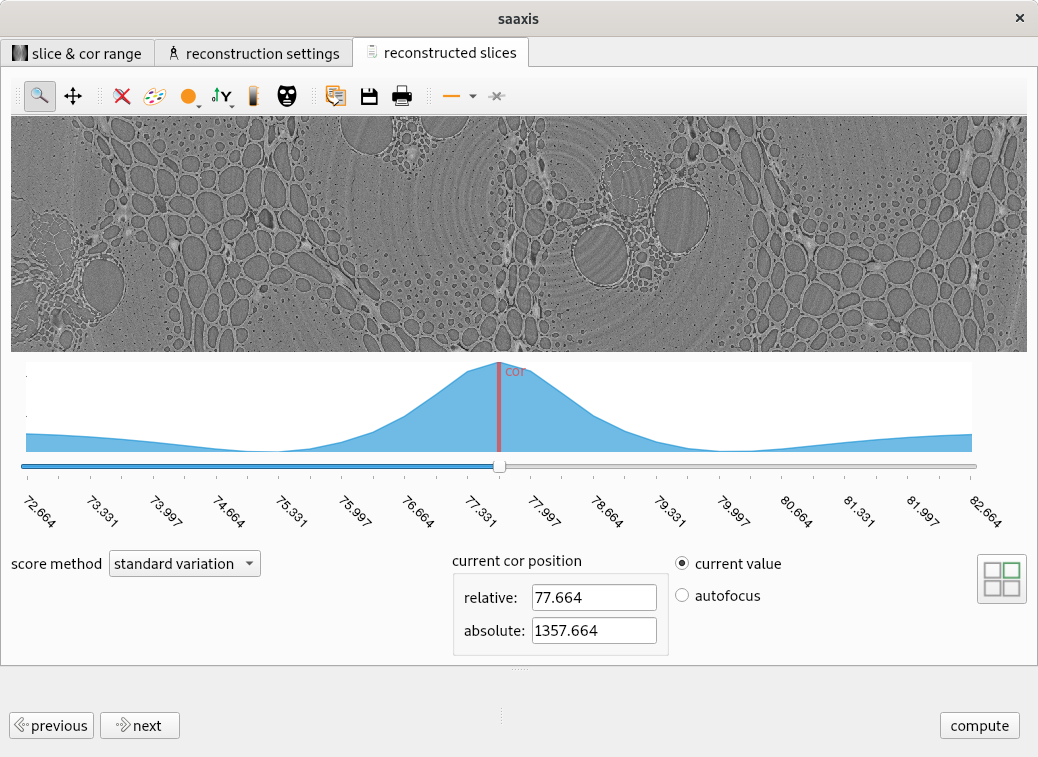
This widget is used to compute the center of rotation to provide to a reconstruction widget (such as Nabu).

It runs a series of slice reconstructions from an “estimated center of rotation” and a width (in pixels). A score will be attributed to each slice (details later).

If the autofocus is locked, it will automatically select the center of rotation that generates the highest score.

If a center of rotation has already been computed upstream (from “axis” or “saaxis” widgets), it will be automatically selected as the “estimated” center of rotation.

You can also call Nabu’s center of rotation search algorithm using the auto cor button.

You can load the sinogram to see the search interval and where the center of rotation will be selected. Since this operation can be time-consuming, interaction is required to load it.

To speed up reconstructions, you can increase the projection subsampling in the Nabu properties (on the reconstruction settings tab) under the reconstruction section. To access this, you need to enable “advanced options.” The option level can be modified via the tool button.

../../../_images/nabu_settings.png

Several saaxis widgets in a workflow#

To automate center of rotation (COR) finding, you can associate several saaxis widgets.

For example, you can use two saaxis widgets in series: * The first widget can deduce a “raw” estimation of the COR (at the pixel level) with a wider search width (several pixels). * The second widget can refine the center of rotation using the estimated COR from the first widget, with a narrower search width (e.g., one pixel).

This is demonstrated in this video.

Score calculation#

Currently, there are two ways to compute a slice reconstruction score. This can be set in the “results” tab:

  • Standard deviation (std): For readability, we multiply the score by 100.

  • Total variation (tv), calculated by the formula:

    \[tv = \sum{\sqrt{\nabla_{x}^2 + \nabla_{y}^2}}\]

    To avoid very low score values, we divide by 10e5.

  • 1 / standard deviation

  • 1 / total variation

  • Tomo consistency:

    We backproject the reconstructed slice for each center of rotation and compute for each COR:

    \[consistency = \sum{ |original\_projections - projection\_recalculated|}\]

    Both original_projections and projection_recalculated are normalized to [0, 1[.

    The score is obtained by:

    \[tomo\_consistency\_score = \dfrac{1}{consistency + 1}\]

The score for std, tv, 1 / std, and 1 / tv is computed on the circumscribed square of the largest common circumscribed circle of all reconstructed slices. Using a square ROI simplifies calculations compared to a disk (for example, gradient calculations).

../../../_images/score_roi.png

Demo#

Several video demonstrations are available: